六角形の美しさとゲーム

身の回りの六角形

ハニカム構造

ハチの巣は正六角形を敷き詰めた構造をしています。
このような構造をハニカム構造といい、少ない材料で高い強度を実現できるという特徴があります。
自然界以外にも、工学の分野で例えば以下のように使われています。

• 航空機やロケットの部品
• 自動車の軽量化材料
• 建築物のファサードパネル
• サッカーのゴールのネット

ゲーム

戦略性が強いボードゲームでは、六角形が敷き詰められたマップ（へクスマップ）がよく使われます。
例えば、カタンというボードゲームでは六角形のマスが敷き詰められてできた島がマップになっています。

日本カタン協会より

また、私もへクスマップが好きで、現時点では以下の2つのゲームでへクスマップを採用しています。

正方形を敷き詰めた碁盤の目のようなマップではなく、なぜわざわざへクスマップを使うのでしょうか？
その理由に迫るために、まずは六角形の性質について紹介します。

六角形の性質

平面充填できる正多角形で一番円に近い

一つの種類の図形で平面を隙間なく敷き詰めることを、ここでは平面充填と呼びます。
平面充填できる正多角形は、正三角形、正四角形、正六角形の三種類しかありません。
これらのうちもっとも角が多い、すなわち円に近いのは正六角形です。
ある方向から衝撃が加えられたときに、辺の数が多い方が衝撃を分散させやすいため、ハニカム構造の強度は高いです。

隣接するマスとの距離が一定

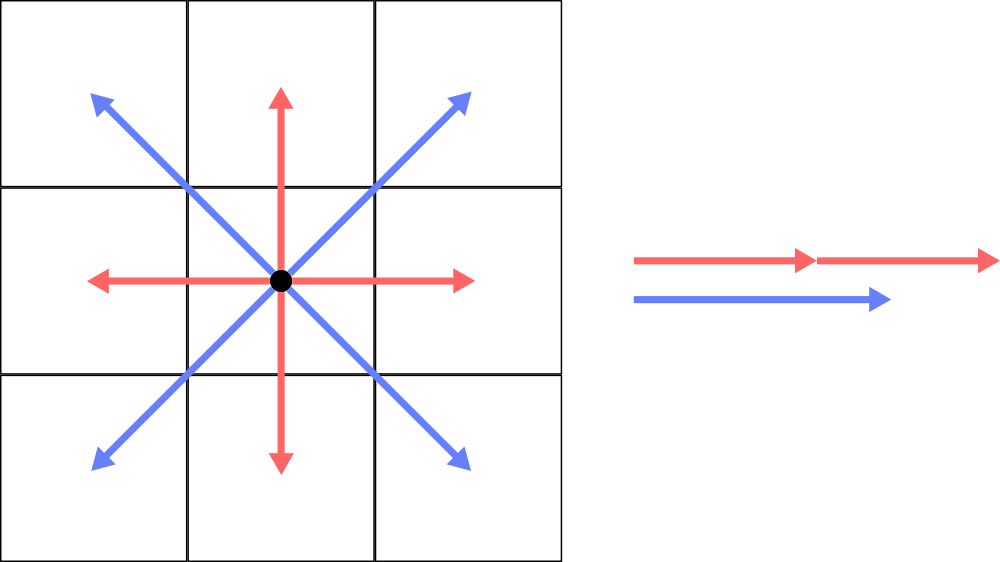
正四角形で敷き詰められたマップは、上下左右のマスとの距離（上の図の赤い矢印の長さ）を$1$とすると、斜めのマスとの距離（上の図の青い矢印の長さ）は$\sqrt{2}$となります。
$\sqrt{2} \fallingdotseq 1.4$なので、ちょうど1と2の中間ぐらいであり、そのため、この斜めのセルの扱いが厄介です。
例えば、戦略シミュレーションゲームで「1マス隣」に攻撃したい場合を考えます。
斜めのマスは直感的には「1マス隣」ではありませんが、かといって2マス隣かという気もしません。
斜めのマスを「1マス隣」とするか「2マス隣」とするかはゲームの製作者に委ねられており、どちらにしても一定の違和感が残ります。
なお、ファイアーエムブレムシリーズでは斜めのマスを「2マス隣」と定義し、射程が2以上の武器でないと攻撃できないようにしていて、そのような扱いとしているゲームが多いように見受けられます。

一方で、正六角形で敷き詰められたマップは、隣接する6マスとの距離がすべて同じです。
これにより、先ほどのような「1マス隣」をどう定義するかという問題は発生しません。
へクスマップはこのように同心円状に広がっていくため、現実の距離感覚に近くなっています。

ゲームとの親和性

先ほど述べたように、へクスマップでは正方形で敷き詰められたマップと違って「1マス隣」をどう定義するかという問題が発生しません。
同心円状に広がっていき、マスとマスの関係が現実の距離感覚に近く、特に戦略性が強いボードゲームと親和性が高いです。

また、ボードゲーム固有の事情として、サイコロとの親和性の高さが挙げられます。
現在最も普及しているサイコロは立方体、つまり正六面体です。
例えば、「サイコロを振って1が出たら右上、2が出たら右、3が出たら右下、…」という具合に各目の値と隣接するセルを一対一に対応付けられるので便利です。

ゲームでの実装

斜交座標

へクスマップの良い性質については前述のとおりですが、一方で、正四角形で敷き詰められたマップと違って、座標を表すのに苦労するという欠点があります。
正四角形で敷き詰められたマップは、直交するX-Y座標を用いて直感的に考えることができますが、へクスマップでは座標をどう考えればよいでしょうか？

一つの方法として、斜交座標を用います。
普通の座標系ではX軸とY軸は直交（すなわち、なす角が90度）しますが、今回は以下のようにX軸とY軸のなす角が60度である斜交座標を考えます。

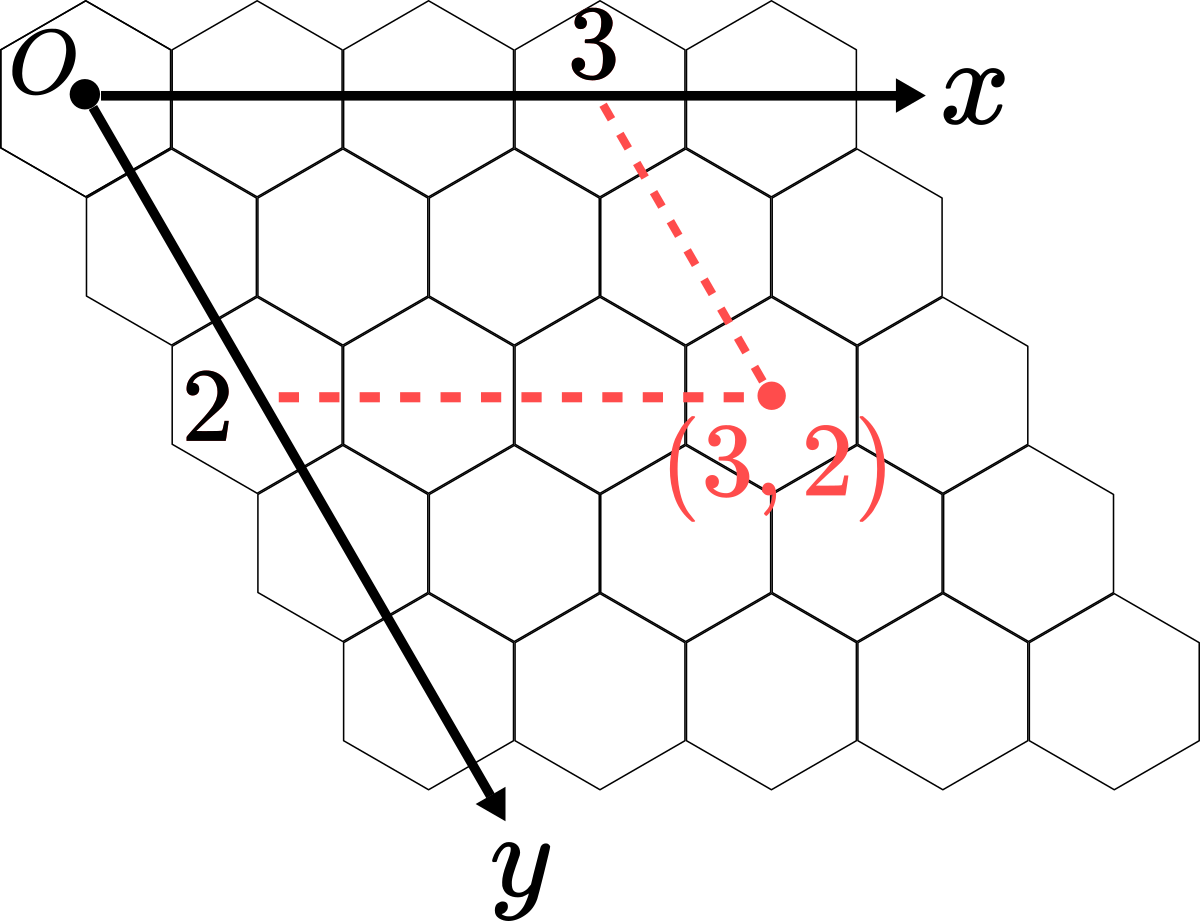
斜交座標に慣れるため、例を考えましょう。
上の図の一番左上のマスを原点$O$とすると、赤色の点の座標はどうなるでしょうか？
原点から数えると、x軸方向に3マス、y軸方向に2マス進めば赤色の点に着くので、座標は$(3,2)$となります。

サンプルコード

では、実際にへクスマップを描画してみましょう。
プログラミング言語はJavaScript、ライブラリはPhaserを用いますが、マニアックなコードは書かないのでご安心ください。
流れとしては、ベクトルを用いて以下の通り処理します。

1. X軸方向とY軸方向の基底ベクトル$\bm{e_x}, \bm{e_y}$を定義する
2. X座標、Y座標についてforループを回す
3. 例えば点$(3, 2)$について、位置ベクトルは$3\bm{e_x}+2\bm{e_y}$となるので、そこを中心に正六角形を描く

サンプルコードは以下の通りです。

  export default class someScene extends Phaser.Scene{
    constructor(){
      ...
    }
    ...
    create(){
      //1.x軸方向とy軸方向の基底ベクトルを定義する
      const o = new Phaser.Math.Vector2(60, 60);  //原点の位置ベクトル
      const e = 50;  //基底ベクトルの長さ
      const e_x = new Phaser.Math.Vector2(e, 0);  //x軸方向の基底ベクトル
      const e_y = e_x.clone().rotate(Math.PI / 3);  //y軸方向の基底ベクトル。x軸方向の基底ベクトルを60度回転させたもの。

      //2.x座標、y座標についてforループを回す
      const x_max = 5;  //x座標の最大値
      const y_max = 5;  //y座標の最大値

      for(let x=0; x<=x_max; x++){
        for(let y=0; y<=y_max; y++){
          //点(x,y)に対応する位置ベクトルを計算
          const pos_x = e_x.clone().scale(x);
          const pos_y = e_y.clone().scale(y);
          const pos = o.clone().add(pos_x).add(pos_y);
          //正六角形を描く。
          //点(x,y)を中心に、60度ずつ回転させながら頂点を設定し、その頂点を結ぶ。
          const points = new Array(); //頂点の位置ベクトルを格納する配列
          //点(x,y)から、正六角形の下の頂点へと向かう位置ベクトル。
          //長さはe/2ではなくe/√3*2となることに注意！
          const e_r = new Phaser.Math.Vector2(0, e / Math.sqrt(3) * 2);
          for(let n=0; n<6; n++){
            const point = pos.clone().add(e_r.clone().rotate(Math.PI / 3 * n));
            points.push(point);
          }
          //6つの頂点を結ぶことで正六角形のポリゴンを作成する
          const hex = new Phaser.GameObjects.Polygon(this, pos.x, pos.y, points, 0xffffff);
          hex.setStrokeStyle(5, 0x000000);  //黒の枠線を設定
          this.add.existing(hex);
        }
      }
    ...
    }
    ...
}

結果は以下の通りです。

最後に

六角形は良い性質を持つ美しい図形であり、その応用範囲は幅広いです。
ゲームに応用するにあたっては、自分で座標系を設定しないといけないので少し大変ではありますが、それを上回るメリットがあると感じています。