空間分割 ~ 近くにあるオブジェクトの検索を高速化する

問題意識

近くにあるオブジェクトの検索

ゲームでは、近くにあるオブジェクトを検索することがしばしばあります。
例えば、以下の図ような空間にオブジェクト（図の黒い点）が散らばっていて、「それぞれのオブジェクトの近くにあるオブジェクトを検索する」という場面は多いと思います。
具体的には、

• 射程範囲内にいるオブジェクトの数を数えたい
• 引力のような力を近くのオブジェクトに作用させたい

などといった場合が想定されます。

そのとき、以下のようにオブジェクトについてforループを二重に回して処理することが多いと思います。

  //オブジェクトについてforループを二重に回す
  for(let i=0; i<objects.length; i++){
    for(let j=0; j<objects.length; j++){
      //i=jの場合は自分なのでスキップする
      if(i === j) continue; 
      //i=jでない場合は、i番目のオブジェクトとj番目のオブジェクトの距離がd以内かどうかを判定する
      if((objects[i].x - objects[j].x) ** 2 + (objects[i].y - objects[j].y) ** 2 <= d ** 2){
        //iとjの距離がd以内である場合の処理
        ...
      } 
    }
  }

計算量の爆発

オブジェクトの数が100個の場合、外側のforループが100回で内側のforループが100回なので、$100 \times 100 = 10,000$回の処理が行われます。
同様の計算で、オブジェクトの数が1,000個の場合は1,000,000回、オブジェクトの数が10,000個の場合は100,000,000回となり、オブジェクトの数の増加に対して計算量が爆発的に増加してしまいます。
上記を定式化すると、「オブジェクトの数が$n$個であるとき、計算量は$O(n^2)$である」と表されます。
これは、「オブジェクトの数の二乗で計算量が増えていく」という意味です。
上記のような計算は、フレームごとなどのかなりの頻度で行いたい場合が多く、オブジェクトが多いと処理落ちしてしまうことがあります。
そこで、以下に紹介する方法で計算量を減らすことができる場合があります。

空間分割

着眼点

例えば、先ほどの図の左下のオブジェクトからしたら、図の右上のオブジェクトなどは明らかに遠すぎます。
上記のコードのforループでは、全てのオブジェクトに対して距離を判定しているので無駄が多いと言えます。
そこで、一度に判定するのではなく、予選と決勝のように判定を二段階に分ければ効率化できそうです。

予選

まず、空間を分割します。
分割する空間のサイズは上記のコードで言うところのdに合わせるのが合理的ですが、今回は図の分かりやすさの観点からいったん5×5のマス目に分割しようと思います。

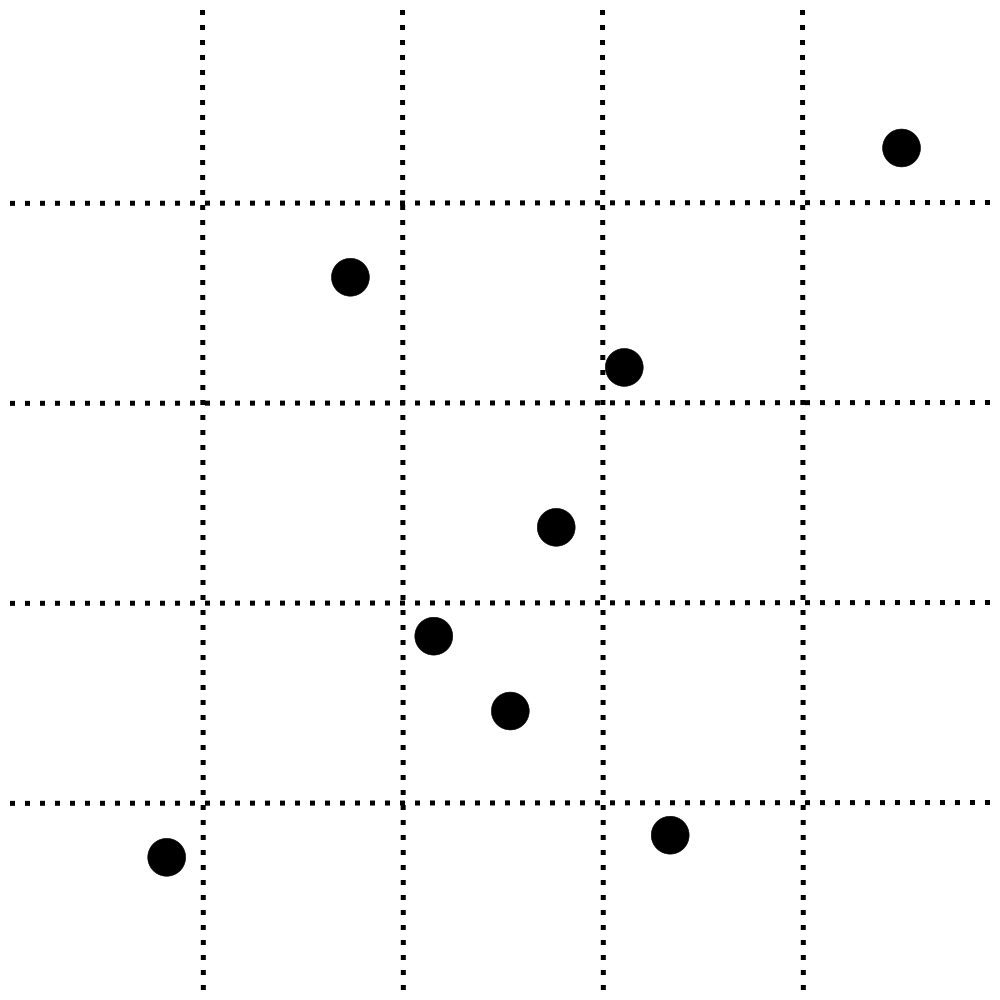
そして、予選として各オブジェクトがどのマスに属しているかを計算します。
これは一回のforループで実行できるので、計算量は$O(n)$で済みます。
空間を分割するにあたって、cellsという三次元配列を導入します。
例えば、cells[3][2]には[objects[2], objects[63], objects[123]]が格納されているとします。
これは、「X軸方向に3番目、y軸方向に2番目のマスには、2番目・63番目・123番目のオブジェクトがある」ということを意味します。

  //cellsの定義
  const cells = new Array(5);
  for(let i=0; i<cells.length; i++){
    cells[i] = new Array(5);
    for(let j=0; j<cells[i].length; j++){
      cells[i][j] = new Array();
    }
  }

  //予選：オブジェクトについてforループを回し、オブジェクトとセルを対応付ける。
  for(let i=0; i<objects.length; i++){
    //今回は空間を縦横に5分割する。5で割ってから端数を切り捨てることで、セルの番地を得ることができる。
    const x = Math.floor(objects[i].x / 5);
    const y = Math.floor(objects[y].y / 5);
    cells[x][y].push(objects[i]);
  }

決勝

次に、それぞれのマスの内部で距離を判定して処理を行います。

  //決勝：それぞれのマスの中で処理を行う
  for(let x=0; x<5; x++){
    for(let y=0; y<5; y++){
      for(let i=0; i<cells[i][j].length; i++){
        for(let j=0; i<cells[i][j].length; j++){
          //i=jの場合は自分なのでスキップする
          if(i === j) continue; 
          //i=jでない場合は、i番目のオブジェクトとj番目のオブジェクトの距離がd以内かどうかを判定する
          if((cells[x][y][i].x - cells[x][y][j].x) ** 2 + (cells[x][y][i].y - cells[x][y][j].y) ** 2 <= d ** 2){
            //iとjの距離がd以内である場合の処理
            ...
          } 
        }
      }
    }
  }

上記のコードをパッと見ると、forループが四重になってしまっています。
しかし、xとyはたった5までだけであり、それに予選を行ったのでcells[i][j]に入っているオブジェクトの数は少なく、明らかに離れているオブジェクトについて距離を判定する機会は劇的に減っていると期待されます。
例えば、$n=100$の場合で、1マスあたり$100\div25=4$個のオブジェクトがある場合、計算量は$5\times 5\times 4\times 4 = 400$回となり、最初の例のように単純にforループを二重に回して全部検索した場合は$100\times 100=10,000$回だったので、大幅に計算量が減っています。

課題

境界の取扱い

あるオブジェクトがマスの端に位置している場合、隣のマスのオブジェクトが近くにある可能性が考えられます。
このような可能性を考慮し、隣のマスのオブジェクトについても距離の判定をするのが安全です。

空間の分割の仕方

今回は空間を均等に分割しましたが、マスによってオブジェクトの密度が高くなったり低くなったりしてしまうことがあります。
そのような場合は、まずは空間をざっくりと分割し、次にオブジェクトの密度が高いマスについては更に分割するというように空間を再帰的に分割するという方法が考えられます。

まとめ

近くにあるオブジェクトを検索するということはしばしばあるので、この方法の使いどころは多いです。
また、上記の例のように空間を均等に分割するだけなら実装が簡単であるのも大きなメリットです。
空間を分割する方法について、上記で少し触れたような再帰的な分割のように様々な方法があるので、機会があればそちらについても記事にしたいです。